電験二種二次試験【機械・制御】攻略法~制御編『出題パターンを物にして完答を目指せ!』

電験二種二次試験【機械・制御】科目は、60分間の試験時間に対し、大問4問中2問を選択し解答します。
【機械・制御】科目では、大問4問中必ず1問は自動制御分野から出題されます。
『自動制御は何だか難しいし、公式覚えるのが大変なので最初から捨てで!』と言う人も多いかもしれません。
が、大問4問の選択問題のうち、最初から自動制御を選択肢から外して残りの機械分野の四機(器)~直流機、誘導機、同期機、変圧器+パワエレクトロニクス だけで勝負するのは、結構リスクがあります。
というのも、誘導機、変圧器については、一見したところサービス問題に見えても実際は計算が鬼ムズで、ドはまりするパターンに陥る可能性が結構あるからです。
また、同期機については、ベクトル図を正確に書けずに撃沈する危険があり、パワエレクトロニクスに至っては問題文の意味が非常にわかり辛く、何度読んでも解法が思いつかないといった可能性があります。
その点、自動制御は公式が複雑ですが、 出題パターンが大体決まっています。
また、電験三種【機械】科目における自動制御の内容をそのまま使える形の出題もかなり見られます。
電験二種二次試験に向けて、新たに覚えなくてはならないのは、
- ラプラス変換
- 二次遅れ要素
- 安定性判別(ラウス・フルビッツ)
位ではないでしょうか?
電験二種二次試験はマークシート方式では無く記述式ではありますが、電験三種の内容をしっかりと理解していれば、それほどハードルは高くないと考えます。
私自身、自動制御が比較的(得意)好きである事もありますが、電験二種二次試験を挑戦される方は、【機械・制御】科目の自動制御分野を是非とも得点源とすることをおススメしたいと思います。
今回は、電験二種二次試験【機械・制御】科目において、自動制御分野に対する出題の傾向、攻略法について攻略法についてまとめてみました。
出題される問題の傾向

電験二種二次試験【機械・制御】 科目の自動制御分野から出題される問題について、下記の問題集及び、試験の問題と解答 | ECEE 一般財団法人電気技術者試験センターのサイトを参考にして過去問の分析を行いました。
自動制御分野からは選択問題4問中毎年1問は必ず出題され、計算問題が100%です。
先述の通り出題パターンが大体決まっているため、試験に向けて方針が立てやすいと言えます。
自動制御分野における出題内容
大問1問につき小問が複数問出題されることが多く、後になればなるほど難しくなる傾向があります。
しかし、殆どにおいて過去問に類似している事が多く、一見して『なんじゃこりゃ!?』という風な問題はほぼ出題されません。
落ち着いて解けば、完答も不可能ではありません。
出題内容は大きく以下のようになります。
伝達関数(殆どがフィードバック制御系)
ブロック線図から伝達関数を求める問題となります。
電験三種【機械】科目でも、同様の問題が多く出題されています。
たいていは、フィードバック制御系における伝達関数を求める形となり基本式である、\( W(s)=\displaystyle \frac{G(s)}{1+G(s)H(s)} \) に当てはめる事によって解けるパターンが多いです。
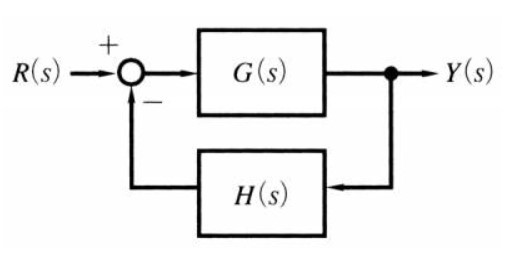

落ち着いて解答し、取りこぼしが無いようにしておきたいところです。
ラプラス変換
ラプラス変換の式
$$F(s)=\mathcal{L}[f(t)] = \displaystyle\int_{0}^{\infty} f(t)e^{-st} dt$$
によって定義される関数により、\( f(t) \Leftrightarrow F(s) \) への変換を用います。
電験二種二次試験を受験される方には、もうおなじみですね。
私の勝手なイメージですが、
【こっちの世界】 \( f(t) \) :t関数 と【あっちの世界】\( F(s) \):s関数を行ったり来たりすることによって扱いづらい物理量(周波数特性)を扱う事が出来る便利な技?
といった感じで理解しています(汗)。
電験三種では出題されていない内容ですが、パターンを掴めばそれほど難しくありません。
定義式により自分で導いても良いですが、この際ラプラス変換表を丸ごと覚えてしまった方が手っ取り早いです。
ラプラス変換の性質として、
- 線形性:\( \mathcal{L}[{af(t)+bf(t)}] = a \mathcal{L}[f(t)]+b \mathcal{L}[f(t)] \)
- 相似性:\( \mathcal{L}[af(t)] = \displaystyle \frac{1}{a} F(\displaystyle \frac{s}{a}) \)
- 第一移動法則:\( \mathcal{L}[e^{at} f(t)] = F(s-a) \)
- 第二移動法則:\( \mathcal{L}[f(t-a)u(t-a)] = e^{-as}F(s) \)
但し、\( u(t-a)=
\begin{cases}
1&(t≧a) \\
0&(t<a)
\end{cases} \)
については、しっかりとマスターしておきたいところです。
加えて、ラプラス変換⇔ラプラス逆変換時には、部分分数展開が必要になるので、これについても合わせてマスターしておきましょう。
ボード線図・ナイキスト線図
電験三種でも多少出題がされていた内容となります。
対数が出てきたり複素数計算が複雑になることが多く、ちょっと苦手に感じられるかもしれませんがこれもだいたい出題パターンは決まっています。
- ボード線図…ゲイン特性のグラフを書く
- ナイキスト曲線…\( ω \)の値によってナイキスト線図の概略を書き、安定性の判別する
といったパターンが多く見られます。
苦手意識を持つことなく、繰返し過去問に触れることにより十分対応可能と考えます。
定常偏差(位置偏差、速度偏差、加速度偏差)
これらは電験三種ではあまり目にしなかった分野かもしれません。
定常偏差については、
- 問題文より伝達関数を求める。
- 入力\( r(t) \)を、ラプラス変換により\( R(s) \)に変換する。
- 入力\( r(t) \) は、殆どの場合、
- 単位インパルス関数:\( r(t)=\delta (t) \ \Rightarrow \ \mathcal{L}[r(t)] = 1 \)
- 単位ステップ関数:\( r(t)=u(t) \ \Rightarrow \ \mathcal{L}[r(t)] = \displaystyle \frac{1}{s} \)
- ランプ関数:\( r(t)=t \ \Rightarrow \ \mathcal{L}[r(t)] = \displaystyle \frac{1}{s^2} \) のいずれか
- 最終値定理を用いて、定常偏差を求める。
- 定常位置偏差…入力:単位ステップ関数 \( \ \Rightarrow \ R(s)=\displaystyle \frac{1}{s} \)
- 定常速度偏差…入力:ランプ関数 \( \ \Rightarrow \ R(s)= \displaystyle \frac{1}{s^2} \)
- 定常加速度偏差…入力:加速度入力\( \ \Rightarrow \ R(s)= \displaystyle \frac{1}{s^3} \)
のパターンで出題されるケースが殆どです。
こちらも同様に、繰返し過去問に触れることにより十分対応可能と考えます。
二次遅れ要素(固有振動数・減衰係数)
これも、電験三種ではあまりお目にかからなかったかもしれませんが、出題パターンとしては、与えられたブロック線図からフィードバック系の伝達関数を求め、二次遅れ要素の標準形:\( W(s)=\displaystyle \frac{{\omega_n}^2}{s^2+2 \zeta \omega_n s+{\omega_n}^2} \)に固有振動数:\( \omega_n \)[rad/s]、減衰係数:\( \zeta \)を代入し、各係数の値を比較する事により解答を導く問題が殆どです。
[H29:問4]なんかは、まさにこのパターンの典型的な出題例となっています。
安定性判別(ラウス、フルビッツ)
安定性判別についても、かなり出やすい傾向にあると言えます。
基本的には、
- ラウス数列を使った安定判別
- フルビッツの行列式を使った安定判別
のいずれかで解ければ良いと考えます。(判別に用いる方法を指定されたことは過去にはありません。)
ラウス数列を使った安定判別の流れは、
- フィードバック制御系の伝達関数を求める。
- 伝達関数の分母を使ってラウス数列を作る。
- ラウス数列の第一列が全て正となるときの条件を求める。
のパターンが殆どといって良いと思われます。繰り返してマスターするようにしましょう。
現代制御
現代制御について、解答するだけであれば高校数学の延長で対応できると考えますが、本質の理解は非常に難しいと言えましょう。
加えて、わかり易くまとまっている書籍や参考書もそれほど多くないように見えます。
私が実際に使ってみてわかり易かった参考書として、こちら👇を紹介します。
電験一種一次試験では、ここ数年もたびたび出題されていますが、電験二種二次試験でも[H28:問4]で出題されています。
ここ10年間の過去問を振り返ってもこの年だけの出題であり、現代制御分野から出題は非常に珍しいと言えるでしょう。
今後も出題される可能性は大いにありそうですが、『こういう問題も出るかも』といった程度で備えておくくらいで良いと考えます。
【機械・制御】~制御科目の攻略法
苦手意識は持たない
冒頭にも述べましたが、自動制御は公式が複雑ですが、 出題パターンが大体決まっています。
また、電験三種【機械】科目の延長上で解ける問題も少なくありません。
食わず嫌いという言葉もありますが、先入観で苦手意識を持たずに、まずはトライしていきながら徐々に自分のモノにしていくことをおススメします。
過去問周回
月並みですが、やはり過去問周回が王道と言えましょう。
繰返し過去問を回しているうちに、ラプラス変換表も自ずと覚えてしまいます。(但し、暫く過去問から離れてしまうとあっという間に忘れてしまいますが…)
日々、継続して過去問に触れる事も重要と考えます。
YouTubeや個人ブログも参考に
最近では、YouTubeでの大学の講義の動画サイトもアップロードされています。また、個人ブログ等でも単元毎に非常にわかり易く解説されているサイトも多く見られます。
自動制御分野において電験二種二次試験に向けて個人的におススメなサイト、YouTubeチャンネルをご紹介します。
こんとろラボ
制御関係における物理数学をはじめ、制御工学の基本について非常にわかり易くまとめられています。
制御工学チャンネル【H.Okajima】
イラストを多用されており、わかりやすい動画チャンネルです。一本の動画が長くても10分程度なので、サクッと視聴することが出来ます。
慶應義塾Keio University 【理工学部講義】制御工学同演習2013
慶応義塾大学の講義の動画です。比較的濃い内容となっております。下記リンクよりYouTubeでご覧下さい。
過去問だけでマンネリ化してしまった場合は、ネット上の解説集を参考にするのも有効と言えましょう。
まとめ
- 電験二種二次試験【機械・制御】科目~制御分野の攻略のポイント
- 苦手意識は持たない⇒電験三種の自動制御+αで対応可能
- 過去問周回が王道⇒出題パターンに慣れましょう!
- YouTubeや個人ブログも有効活用⇒市販の電験向けの参考書に比べて非常にわかり易いサイトが多数あり!
今回はここまでとさせて頂きます。
最後まで読んで頂き、ありがとうございました。











